A06：1000T非摂動磁場効果の理論

研究概要

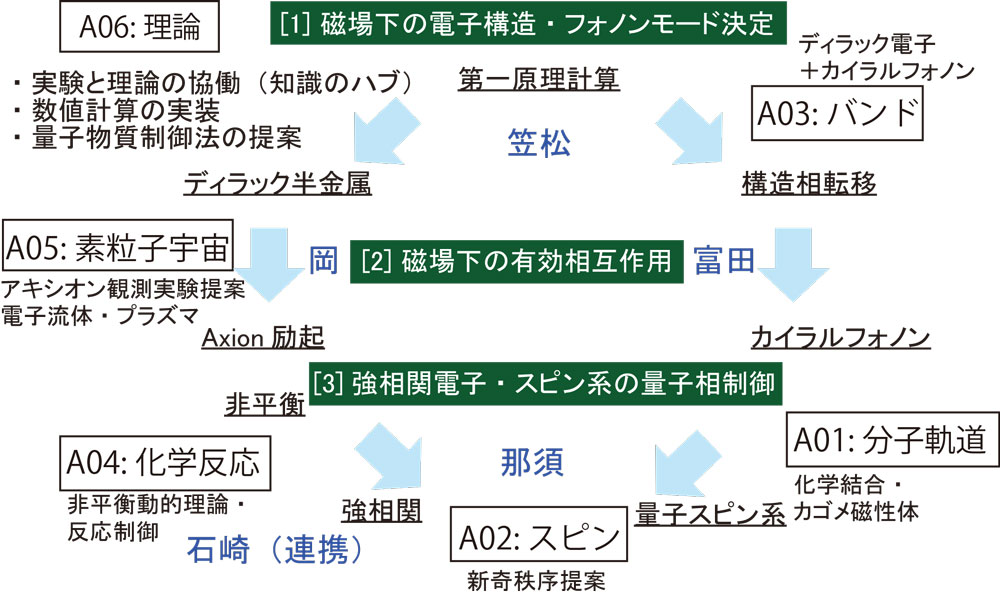
理論班には領域代表からは階層を超えた磁場中物理の学術変革の基盤となる理論構築という高い目標を与えられました。紀元前の磁石の発見に端を発した磁場下の物理は、近現代では電磁気学や量子電磁力学の確立の指針を与え、物性ではランダウ量子化や整数・分数量子ホール効果、ホフスタッターバタフライの発見に至るなど非常に長く深い研究の歴史があります。本領域ではこれらに匹敵するマイルストーンとなる発見が求められます。本領域と関係の深い電場中の固体物理や、素粒子のアキシオン探索、そして分子やタンパク質の量子化学的研究における進展を取り込みつつ、シンプルで普遍的な系を考えることで前進したいです。

並行世界としての電場中物理

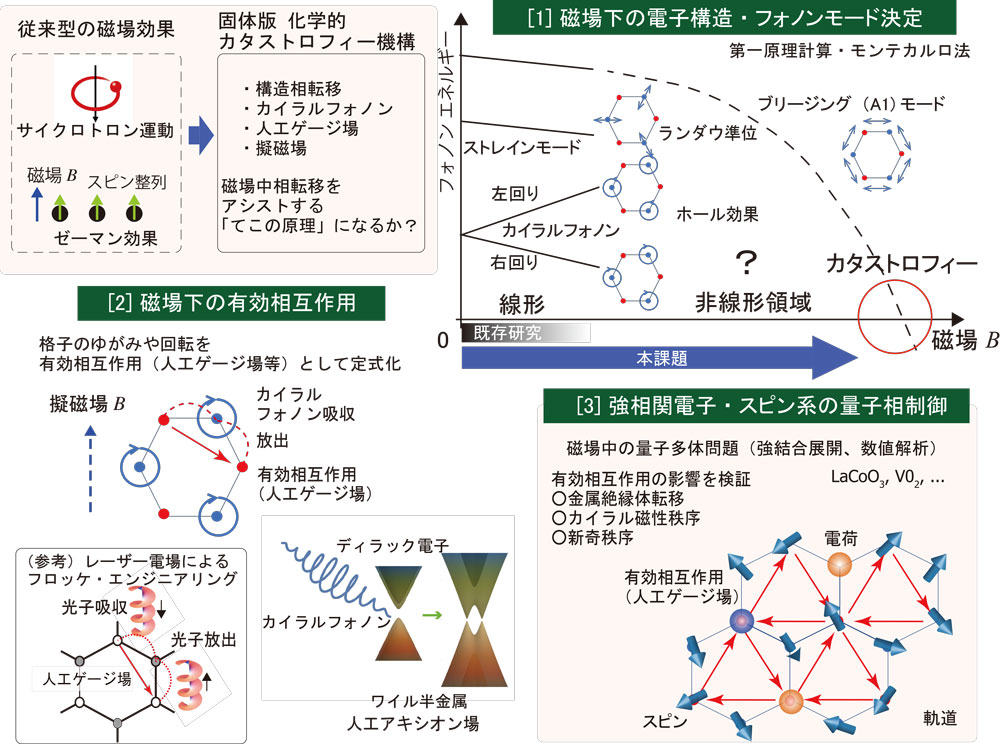
現在、電場中の物理は量子幾何学効果のキーワードの下に現代化の途上にあります。幾何学効果は平易にいうとハミルトニアンが行列であることに由来する現象です。ベリー曲率由来の量子ホール効果やカイラル磁気効果、アキシオン応答などが代表例です。幾何学効果は絶縁体の起金属転移にも現れます。絶縁体に電場を印可すると、まず分極が誘起され、次にシュインガー機構により電子・正孔の対生成が起きます。さらに強電場では、電子はワニエ・シュタルク局在状態に移行します。近年は非熱的量子制御をめざし、電子を光子と結合させバンド構造そのものを制御するフロッケ・エンジニアリングや格子を電場で制御する非線形フォノニクスが発展しております。磁場は電場と同じくゲージ場として電子と相互作用するため各現象には磁場誘起の対応物があり、本研究で参考にしたいです。

磁場中物理のミニマル問題

① ランダウ量子化と量子幾何学効果、非可換場の理論

ランダウ量子化と量子幾何学効果が結びつくと特異な量子現象が発現します。ディラック電子における真空偏極やカイラル磁気効果、平坦バンド系における量子計量と関連した現象 (Nature 584, 59(2020))が知られています。本領域で興味を持たれているディラック絶縁体やファン・ホーフ特異性のある系（Sr₂RuO₄等）などにも未知の量子現象が隠れているかもしれません。磁場中の量子系はランダウ準位（非可換場の理論）で記述され、ポテンシャル問題やエキシトン等の束縛準位の解析が容易になりますが、量子幾何学効果を取り込む研究に余地があります。

② ホフスタッターバタフライと相関効果

1000Tの磁気長は8Å程度です。同程度の格子定数を持つフラーレン固体や分子性導体ではホフスタッターバタフライが現れます。これらの物質群では超伝導や電荷秩序、モット転移などの強相関秩序が発現するため磁場下の相関効果を調べる理想的な舞台です。これらの系を念頭に強相関模型を用いたトポロジカル秩序等の量子多体相の探索を考えております。

③ 固体の化学的カタストロフィー

本領域では既に磁場の印可によって結晶構造やスピン構造が破壊的に変化する固体版の化学カタストロフィーが実現しております。一方で、そのメカニズムの詳細は未解明で、理論研究も乏しいです。格子自由度は電子と結合することで数千倍に増強された磁場効果を受けることがカイラルフォノンの研究で知られています。この知見を元に、磁場誘起相転移における「てこの原理」を探索します。

④ カイラルフォノンとフロッケ・エンジニアリング

電子・光子系ではフロッケエンジニアリングや共振器エンジニアリングに注目が集まっています。これを磁場下の電子・格子系に翻訳すると、カイラルフォノンと結合した電子のフロッケ状態やポーラロン状態と、そこで発生するホール効果やカイラル秩序の問題になります。

⑤ 階層を越えて-“アキシオン探索からタンパク質・分子系へ”-

アキシオン探索に物性側から参画するチャンスをうれしく感じます。未知素粒子としてのアキシオンはディラックフェルミオンの軸性電流と結合するスカラー場です。一方で、物性の広義のアキシオンはベリー曲率由来のホール効果を誘起する準粒子一般で、磁性ワイル半金属のマグノンやフォノン、エキシトンなど多様です。物性には準粒子を測定する様々なノウハウがありますので、うまく意思の疎通ができれば新しいアキシオン探索方法を提案できるかもしれません。さらにはタンパク質や分子を含む非晶質の磁場効果には環状電流やCISをはじめとした興味深い問題が多くあります。極限的な磁場下でのシンプルな設定を考えることで新しい視点を得たいです。

研究成果

原著論文

学会発表